Chapitre 2 - Suites
Question n°1: Pour toutes suites (Un) et (Vn), et ![]() une fonction telle que Vn =
une fonction telle que Vn = ![]() on a :
on a :
(Vn) est une sous-suite de (Un) si et seulement si :
A. | |
B. (Un) monotone
| |
C. (Vn) monotone
| |
D. | |
Question n°2:
On utilise des suites extraites surtout pour :
A. faire plaisir à Mr Habib
| |
B. pour démontrer qu'une suite n'a pas de limite
| |
C. pour démontrer qu'une suite est convergente
| |
D. Pour faciliter les calculs.
| |
Question n°3:
Quelles sont les affirmations vraies, s'il y en a?
A. | |
B. (Un) stationnaire => (Un) constante
| |
C. | |
Question n°4:
Pour montrer qu'une suite est convergente en ayant recours à la définition première de la limite, il faut:
A. Avoir une idée de la limite
| |
B. Obtenir une inégalité du type p >...
| |
C. Obtenir une inégalité du type p< ...
| |
Question n°5:
Les affirmations suivantes sont-elles vraies (cocher la case correspondante si c'est le cas)?
A. (cos(n)) est divergente
| |
B. pour toute suite (Un): (Un) tend vers +
| |
Question n°6:
Pour toute suite (Un) convergente vers un réel l, on a:
Question n°7:
La limite de la forme ![]() vaut :
vaut :
A. 1
| |
B. e
| |
C. 0
| |
D. | |
E. pas de limite
| |
Question n°8:
![]() tend en +
tend en +![]() vers :
vers :
A. rien
| |
B. 1
| |
C. + | |
D. e
| |
E. 0
| |
Question n°9:
Pour toute suite de Cauchy (Un), on a:
A.(Un) converge
| |
B. | |
Question n°10:
Quelle étape de la méthode pour déterminer qu'une suite est une suite de Cauchy est fausse?
A. Démontrer que | |
B. Montrer que : | |
C. D'où : | |
D. Arriver à : | |
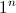
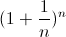
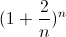
 . Ainsi on ne peut rien conclure car on peut aboutir à n'importe quel résultat.
. Ainsi on ne peut rien conclure car on peut aboutir à n'importe quel résultat.